দশম শ্রেণির গণিত এসাইনমেন্ট ২০২২ সমাধান ১ম সপ্তাহ

 

দশম শ্রেণির গণিত এসাইনমেন্ট ২০২২ সমাধান ১ম সপ্তাহ

প্রিয় দশম শ্রেণীর শিক্ষার্থীরা তোমাদের জন্য নিয়ে এলাম দশম শ্রেণির গণিত এসাইনমেন্ট ২০২২ সমাধান ১ম সপ্তাহ। এখানে তোমাদের ১ম সপ্তাহের এসাইনমেন্ট গনিত প্রশ্নগুলোর উত্তর সুন্দরভাবে উপস্থাপন করা হয়েছে।

দশম শ্রেণির গণিত এসাইনমেন্ট ১ম সপ্তাহ ২০২২

Table of Contents

• 1.দশম শ্রেণির গণিত এসাইনমেন্ট ১ম সপ্তাহ ২০২২
• 1.1.দশম শ্রেণির গণিত এসাইনমেন্ট ২০২২ প্রশ্ন
• 1.2.দশম শ্রেণির এসাইনমেন্ট গণিত ১ম সপ্তাহ সমাধান
• 1.2.1.গণিত অ্যাসাইনমেন্ট ২০২২

দশম শ্রেণীর অ্যাসাইনমেন্ট ২০২২ তোমাদের মাধ্যমিক ও উচ্চ শিক্ষা অধিদপ্তর থেকে দেওয়া হয়েছে প্রথম সপ্তাহের জন্য। করোনাকালীন সময়ে ২০২২ সালে এটি তোমাদের প্রথম অ্যাসাইনমেন্ট। ২০২২ সালের প্রথম সপ্তাহের অ্যাসাইনমেন্ট তোমাদের দুটি বিষয়ের উত্তর লিখতে হবে একটি হচ্ছে বাংলা ও অপরটি সাধারণ গণিত।

আজকে আমরা তোমাদের ১০ম শ্রেণির এসাইনমেন্ট ২০২১ গণিত ১ম সপ্তাহ এর একটি নমুনা উত্তর প্রদান করব। এই উত্তরটি তোমরা সরাসরি তোমাদের অ্যাসাইনমেন্ট উত্তরপত্রে লিখতে পারো কারণ গণিতের ক্ষেত্রে নিজে থেকে বানিয়ে লেখার কোনো সুযোগ নেই। তবে কিছু কিছু শব্দ তোমরা নিজেদের মতো করে পরিবর্তন করে নিতে পারো।

গণিত অ্যাসাইনমেন্ট ১০ম শ্রেণী প্রথম সপ্তাহ ২০২২ তোমাদের জ্যামিতি অংশ থেকে দেয়া হয়েছে। এখানে তোমাদের চারটি প্রশ্ন দেওয়া হয়েছে যার উত্তর যথাযথভাবে তোমাদের দিতে হবে। তোমরা যারা দশম শ্রেণীর শিক্ষার্থী তারা অধিকাংশই গণিত অ্যাসাইনমেন্ট এর প্রশ্ন গুলো না পড়েই উত্তর লেখা শুরু করে দাও যেটা মোটেই কাম্য নয়। তাই তোমাদের কাছে অনুরোধ থাকবে তোমরা অবশ্যই প্রশ্নটিই সুন্দরভাবে পড়বে এবং বুঝে নমুনা উত্তর দেখে নিজেরাই করার চেষ্টা করবে।

তো চলো শিক্ষার্থী বন্ধুরা আমরা প্রথমে ২০২২ সালের গণিত অ্যাসাইনমেন্ট প্রথম সপ্তাহের প্রশ্ন গুলো দেখে নেই।

দশম শ্রেণির গণিত এসাইনমেন্ট ২০২২ প্রশ্ন

গণিত অ্যাসাইনমেন্ট নম্বর ১ দশম শ্রেণি

১০ম শ্রেণির গণিত অ্যাসাইনমেন্ট (শিরোনাম)ঃ

বৃত্ত সংক্রান্ত উপপাদ্য প্রমাণ ও প্রয়োগ

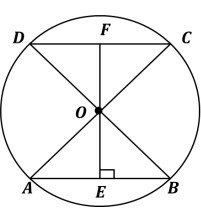
চিত্রে AB=CD এবং AB||CD

১০ম শ্রেণির ১ম সপ্তাহের এসাইনমেন্ট শিখনফল/ বিষয়বস্তুঃ

১। বৃত্ত সংক্রান্ত উপপাদ্য প্রমাণ করতে পারবে।
২। বৃত্ত সংক্রান্ত বিভিন্ন সমস্যা সমাধানে উপপাদাগুলো প্রয়োগ করতে পারবে।

দশম শ্রেণির এসাইনমেন্ট প্রণয়নের নির্দেশনা (ধাপ/পরিধি/সংকেত):

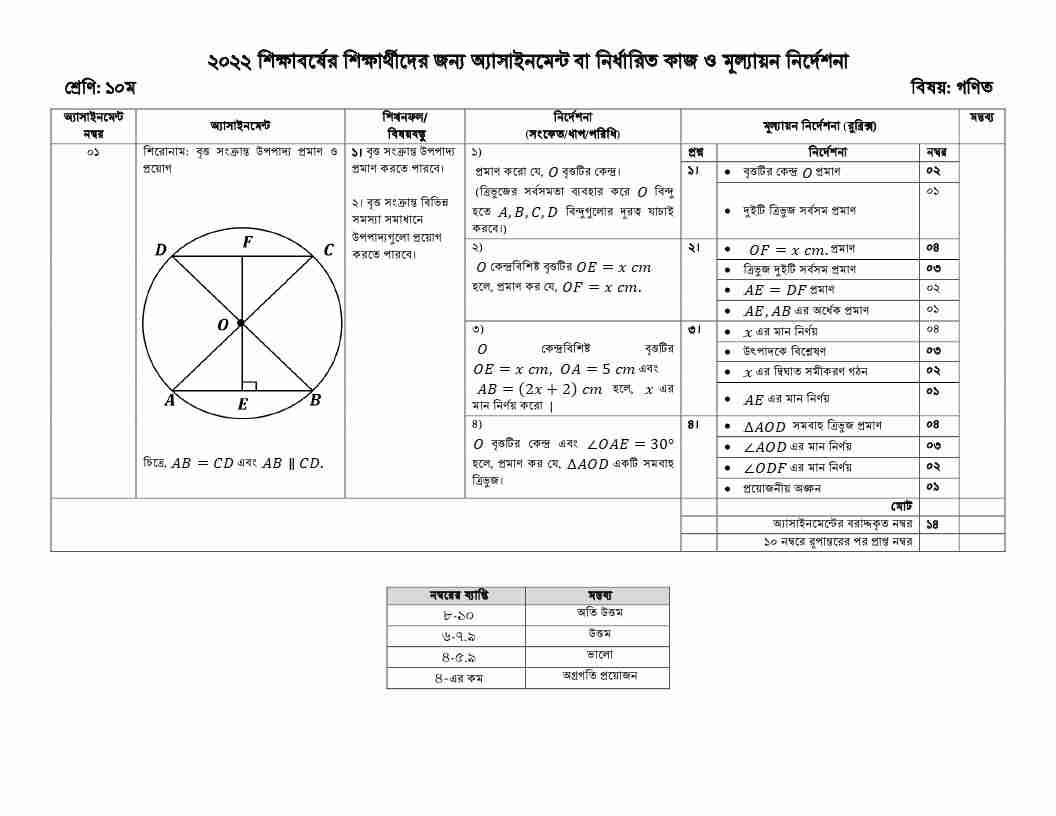
১) প্রমাণ করো যে O  বৃত্তটির কেন্দ্র (ত্রিভুজের সর্বসমতা ব্যবহার করে O  বিন্দু হতে A,B,C,D  বিন্দু গুলোর দূরত্ব যাচাই করবে)

২) O কেন্দ্র বিশিষ্ট বৃত্তটির OE =x cm  হলে প্রমাণ করো যে OF=x cm

৩) O  কেন্দ্র বিশিষ্ট বৃত্তটির OE =x cm, OA=5cm  এবং AB=(2x+2) cm  হলে x  এর মান নির্ণয় করো।

৪) O  বৃত্তের কেন্দ্র এবং ∠OAE =300  হলে, প্রমাণ করো যে ΔAOD  একটি সমবাহু ত্রিভুজ।

উপরের প্রশ্ন গুলো দেখে তোমরা নিশ্চয়ই বুঝতে পারছ তোমাদের জ্যামিতি চিত্র সহ প্রমাণ করতে হবে। চারটি ধাপে গণিত অ্যাসাইনমেন্ট ২০২২ দশম শ্রেণি এর উত্তর লিখতে হবে। আমরা তোমাদের এখানে একটি নমুনা উত্তর প্রদান করছি যেটি সুন্দরভাবে এবং মনোযোগ সহকারে করা হয়েছে। তোমরা নিচের উত্তরটি সম্পূর্ণ পড়ে তারপর তোমাদের অ্যাসেসমেন্ট খাতায় লেখা শুরু করবে।

দশম শ্রেণির এসাইনমেন্ট গণিত ১ম সপ্তাহ সমাধান

অ্যাসাইনমেন্ট শুরু

১নং প্রশ্নের উত্তর

মনেকরি, ABCD বৃত্তের AB ও CD দুইটি জ্যা এবং AB = CD এবং  AB|| CD। প্রমাণ করতে হবে যে, 0 বৃত্তের কেন্দ্র।

প্রমাণঃ

যেহেতু AB||CD এবং AC তাদের ছেদক।
সুতরাং ∠BAC=∠ACD [ একান্তর কোণ]

বা, ∠BAO = ∠OCD

আবার , যেহেতু AB||CD এবং BD তাদের ছেদক
সুতরাং ∠ABD = ∠BDC [ একান্তর কোণ]
∠ABO = ∠ODC

এখন ,ΔOAB এবং ΔOCD এর মধ্যে  AB = CD,

এবং ∠ABO = ∠ODC

এবং ∠BAO = ∠OCD

সুতরাং ΔOAB ও ΔOCD সর্বসম ত্রিভুজ।

∴ ΔOAB ≅ ΔOCD

∴ ‍AO = CO এবং BO = DO

আবার ∠BEO =900 [দেওয়া আছে]

∴  ‍∠AEO =900 [সম্পুরক কোন]

∴  ‍∠BEO = ∠AEO

তাহলে Δ DOC এ CO = DO

∴ AO = CO = DO = BO

অর্থাৎ O বিন্দুটি A,B,C,D হতে সমদুরবর্তী

∴ O বিন্দুই বৃত্তের কেন্দ্র (প্রমাণিত)

২নং প্রশ্নের উত্তর

Δ ‍AEO এবং Δ BEO এর জন্য

OE = OE [সাধারণ বাহু]

AO = BO [১নং হতে]

∴ Δ AEO ও ΔBEO সর্বসম [অতিভুজ বাহু উপপাদ্য অনুযায়ী]

অর্তাৎ ΔAEO≅ ΔBEO

সুতরাং AE = BE অর্থাৎ E, AB এর মধ্যবিন্দু

∴ BE =  AB

একইভাবে ΔDOF এবং ΔCOF এ DF =  CD

যেহেতু AB = CD [দেওয়া আছে]

∴   AB =  CD

বা BE = DF

এখন ΔBOE এবং ΔDOF এ

BF = DF

BO = DO [১নং হতে পাই]

∠EBO = ∠FDO

∴ ΔBOE≅ ΔDOE

∴ OE = OF

যেহেতু OE = x cm তাই OF = x cm (প্রমাণিত)

৩নং প্রশ্নের উত্তর

দেওয়া আছে,

O কেন্দ্র বিশিষ্ট বৃত্তটির OE = x cm

OA = 5 cm

AB = (2x+2) cm

AB এর মধ্যবিন্দু E, তাহলে AE=BE

সুতরাং AE = 

∴AE = (x+1) cm

Δ AEO সমকোনী ত্রিভূজ। 

সুতরাং পিথাগোরাসের সূত্রানুসারে পাই

OA2 = OE2 + AE2

বা, 52= x2 +(x+1)2

বা, 25 = x2 +x2 +2x+1

বা, 25 = 2x2 +2x+1

বা,  2x2 +2x+1 = 25

বা,  2x2 +2x+1 -25 = 0

বা,  2x2 +2x -24 = 0

বা,  2(x2 +x-12) = 0

বা,  (x2 +x-12) = 0

বা, x2 +4x-3x-12 =0

বা, x(x+4)-3(x+4) =0

বা, (x+4)(x-3) =0

হয়, x+4 = 0        অথবা, x-3=0

∴ x=-4                        ∴ x=3

গ্রহনযোগ্য নয়

অতএব x এর মান 3 cm (উত্তর)

৪নং প্রশ্নের উত্তর

১নং হতে পাই ΔAOB ≅ ΔODC 

তাহলে ∠ODC = 300 হবে।

অর্থাৎ ∠ ODF = 300

তখন, ΔAEO এর জন্য

∠A+∠B+∠AOE = 1800

বা, 900+300+∠AOE = 1800

বা, ∠AOE = 1800-1200

∴ ∠AOE = 600

অনুরুপভাবে ΔDOF এ, ∠DOF =900

এখন, ∠AOE+∠AOD+∠DOF = 1800

বা, 600+∠AOD +600 = 1800

বা, ∠AOD = 1800-1200

∴ ∠AOD = 600

আবার, ∠DAE = ∠DAO+∠OAE

বা, 900 = ∠DAO +300

বা, ∠DAO = 900-300

∴ ∠DAO = 600

অতএব অনুরুপভাবে ∠ADO = 600

Δ AOD এর তিনটি কোণ ∠DAO =600, ∠ADO =600, ∠AOD =600

সুতরাং Δ AOD একটি সববাহু ত্রিভূজ। (প্রমাণিথ)

অ্যাসাইনমেন্ট শেষ

উপরের দশম শ্রেণীর গণিত অ্যাসাইনমেন্ট ২০২২ এর উত্তরটি তোমাদের পছন্দ হলে তোমরা তোমাদের বন্ধুদের সাথে শেয়ার করবে। সেইসাথে উত্তরটিতে কোন প্রকার ত্রুটি থাকলে অথবা তোমাদের কোন জিজ্ঞাসা থাকলে তোমরা অবশ্যই কমেন্ট করে জানাবে।

Class 10 Assignment 1st weak Bangla